Diagram Venn
 |
| Diagram Venn yang ditemukan oleh John Venn |
Diagram Venn adalah diagram adalah diagram yang menunjukkan semua kemungkinan hubungan logika dan hipotesis di antara sekelompok (set/himpunan/grup) dengan benda/objek yang digunakan untuk mewakili himpunan, hubungan antara himpunan dan operasi yang dilakukan padanya dengan cara bergambar berbentuk lingkaran. Sebagai ilmu matematika, diagram Venn ini pertama kali diperkenalkan pada tahun 1880 oleh John Venn untuk menunjukkan hubungan sederhana dalam topik-topik di bidang logika, probabilitas, statistik, linguistik dan ilmu komputer. Diagram Venn, yang diperkenalkan oleh John Venn (1834-1883), menggunakan lingkaran (tumpang tindih, berpotongan dan tidak berpotongan) untuk menunjukkan hubungan antara himpunan. Diagram Venn juga disebut diagram himpunan atau diagram logika yang menunjukkan operasi himpunan yang berbeda seperti persimpangan himpunan, penyatuan himpunan, dan perbedaan himpunan. Ini juga digunakan untuk menggambarkan subset dari satu set/kumpulan.
HAL YANG PERLU DIPERHATIKAN DALAM MEMBUAT DIAGRAM
VENN
Berikut adalah beberapa hal yang harus kita perhatikan dalam menggambar suatu Diagram Venn
- Buatlah persegi panjang atau persegi.
- Himpunan semesta digambarkan dengan persegi panjang dan lambang S yang mana
ditulis pada sudut kiri atas dalam gambar persegi panjang. Himpunan semesta (S) adalah
himpunan yang memuat semua anggota himpunan yang dibicarakan.
- Setiap himpunan lain yang dibicarakan digambarkan dengan lingkaran (kurva tertutup)
kecuali yang tidak termasuk dalam himpunan lain yaitu dituliskan diluar lingkaran.
- Setiap anggota ditunjukkan dengan noktah (titik) dan anggota himpunan ditulis di
samping noktah tersebut.
MACAM-MACAM HIMPUNAN PADA DIAGRAM VENN
Himpunan yang Berpotongan
Himpunan A dan B saling berpotongan jika ada anggota himpunan A dan B yang sama.
Himpunan A berpotongan dengan himpunan B dapat ditulis dengan A∩B. Himpunan yang
berpotongan dapat dinyatakan dengan diagram Venn pada Gambar dibawah ini
Contoh soal:
Tentukanlah himpunan dari diagram venn berikut
Jawaban:
Dengan mudah dapat kita jawab sebagai berikut
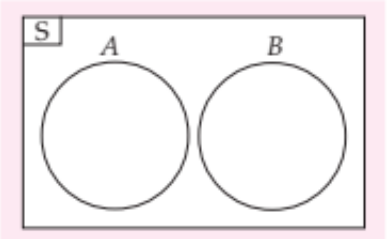
Himpunan A dan B dikatakan saling lepas apabila tidak ada anggota himpunan A dan B yang
sama. Himpunan A saling lepas dengan himpunan B dapat ditulis A//B. Himpunan saling
lepas dari himpunan A dan B dinyatakan dengan diagram Venn seperti pada Gambar di
bawah ini
Himpunan Bagian
Himpunan A dapat dikatakan himpunan bagian dari himpunan B jika semua anggota
himpunan A merupakan anggota dari himpunan B. Himpunan A merupakan himpunan
bagian dari himpunan B dapat dinyatakan dengan diagram Venn seperti pada Gambar di
bawah ini
Himpunan Yang Sama
Himpunan A dan B dikatakan himpunan yang sama jika setiap anggota A merupakan anggota B
dan setiap anggota B merupakan anggota A. Misalnya A = {1, 2, 3} dan B = {3, 2, 1} dapat
dikatakan himpunan A sama dengan himpunan B dan dapat ditulis A = B. Dengan diagram Venn
dapat dinyatakan seperti pada Gambar dibawah ini
Himpunan Yang Ekuivalen
Dua himpunan dikatakan ekuivalen apabila jika ada banyaknya anggota dari kedua himpunan
tersebut adalah sama. Contoh: A = {a, b, c, d}; B = {1, 2, 3, 4} A dan B dikatakan himpunan
yang ekuivalen. Himpunan A ekuivalen dengan himpunan B jika:n(A) = n(B)
ISTILAH DALAM HIMPUNAN
Dalam Himpunan kita mengenal beberapa istilah seperti irisan, gabungan dan selisih serta
komplemen.
Irisan Himpunan
Irisan dari dua himpunan A dan B adalah himpunan yang anggota-anggotanya ada di himpunan A dan ada di
himpunan B. Bisa dikatakan himpunan yang anggotanya ada di kedua himpunan tersebut.
Contoh: A = {a, b, c, d, e} dan B = {b, c, f, g, h}
Pada kedua himpunan tersebut ada dua anggota yang sama yaitu b dan c. Oleh karena itu, dapat dikatakan
bahwa irisan himpunan A dan B adalah b dan c atau ditulis dengan:
A ∩B = {b, c}
A∩B dibaca himpunan A irisan himpunan B. Dengan diagram Venn A∩B dapat dinyatakan seperti pada
Gambar di bawah ini.
Gabungan Himpunan
Gabungan dari dua himpunan A dan B merupakan suatu himpunan yang anggota-anggotanya ialah anggota himpunan A atau anggota himpunan B atau anggota kedua-duanya.
Contoh:
A = {1, 2, 3, 4} dan B = {4, 5, 6, 7}
Gabungan dari kedua himpunan A dan B adalah {1, 2, 3, 4, 5, 6, 7} atau dapat ditulis:
A ᴗB = {1, 2, 3, 4, 5, 6, 7}
AᴗB dibaca himpunan A gabungan himpunan B. Dengan begitu diagram Venn, AᴗB ditunjukkan
oleh Gambar berikut.
Komplemen
Komplemen dari himpunan A adalah himpunan yang anggota-anggotanya bukan merupakan
anggota himpunan A.
Contoh: S = {0, 1, 2, 3, 4, 5, 6, 7}
A = {2, 3, 4, 5}
Komplemen dari himpunan A adalah {0, 1, 6, 7}. Komplemen dari himpunan A dinotasikan
atau ditulis A’ dibaca A komplemen atau komplemen dari A. Komplemen A juga dapat
dinyatakan dengan diagram Venn. Diagram Venn dari A’ dinyatakan seperti Gambar berikut:
CONTOH SOAL DIAGRAM HIMPUNAN
Perhatikan diagram Venn Di bawah ini :