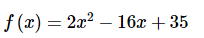Apa Itu Turunan (Derivatif)

Pendahuluan

    Hennessey Venom GT adalah salah satu mobil tercepat di dunia. Pada tahun 2014, ia mencapai kecepatan rekor 270.49 mph. Itu bisa berubah dari 0 hingga 200 mph dalam 14,51 detik. Dengan itu postingan kali akan membahas perhitungan yang dapat digunakan untuk menghitung percepatan yang dicapai Venom dalam prestasi ini.)

Hennessey Venom GT dapat melaju dari 0 hingga 200 mph dalam 14,51 detik.

    Menghitung kecepatan dan perubahan kecepatan adalah penggunaan kalkulus yang penting, tetapi jauh lebih luas dari itu. Kalkulus penting di semua cabang matematika, sains, dan teknik, dan sangat penting untuk analisis dalam bisnis dan kesehatan juga. Dalam postingan ini, kami mengeksplorasi salah satu alat utama kalkulus, turunan, dan menunjukkan cara yang nyaman untuk menghitung turunan.

    Pada bagian postingan saya bab Limits kita telah melihat dan mengetahui bahwasanya perhitungan kemiringan garis singgung, laju perubahan fungsi secara cepat, dan kecepatan sesaat suatu objek pada x=a semua itu  dapat kita hitung dengan menggunakan defenisi limit berikut

$x=\mathrm{sebuah}$

Kita juga melihat bahwa dengan sedikit perubahan notasi limit ini juga dapat ditulis sebagai,

Ini adalah limit yang sangat penting dan muncul di banyak tempat pada persamaan matematika sehingga disepakati dengan memberinya nama yaitu istilah turunan. Berikut adalah definisi resmi dari apa itu turunan.

Definisi Turunan (Derivatif)

Turunan dari $f\left(x\right)$ sehubungan dengan x adalah fungsinya $f^{\prime }\left(x\right)$ yang didefinisikan sebagai,

Perhatikan bahwa kita mengganti semua a di $\text{(1)}$ dengan x untuk mengakui fakta bahwa turunannya benar-benar fungsi juga. Kita sering "membaca" $f^{\prime }\left(x\right)$ sebagai "f aksen x".

Mari kita hitung beberapa contoh soal turunan menggunakan definisi tersebut.

Contoh Soal dan Penyelesaian

Contoh 1 Tentukan turunan dari fungsi berikut menggunakan definisi turunan.

Jawab:

Jadi, yang benar-benar perlu kita lakukan adalah memasukkan fungsi ini ke dalam definisi turunannya seperti pada persaman $\text{(2)}$, dan lakukan beberapa perhitungan aljabar. Meskipun, memang, aljabar kadang-kadang akan menjadi agak tidak menyenangkan, tetapi itu hanya aljabar jadi jangan bersemangat tentang fakta bahwa kita sekarang menghitung turunannya.

Pertama-tama masukkan fungsi ke dalam definisi turunan yaitu:

Berhati-hatilah dan pastikan bahwa Anda menangani tanda kurung dengan benar saat melakukan pengurangan.

Sekarang, kita tahu dari bab sebelumnya bahwa kita tidak bisa begitu saja mencolokkan $h=0$ karena ini akan memberi kita pembagian dengan nol kesalahan. Jadi, kita harus melakukan beberapa pekerjaan. Dalam hal ini itu berarti mengalikan semuanya dan mendistribusikan tanda minus melalui pada periode kedua. Sehingga dapat kita hitung,

Perhatikan bahwa setiap istilah dalam pembilang yang tidak memiliki h di dalamnya dibatalkan dan kita sekarang dapat memperhitungkan h dari pembilang yang akan membatalkan terhadap h dalam penyebut. Setelah itu kita bisa menghitung batasnya.

Jadi, turunannya adalah,

Contoh 2 Tentukan turunan dari fungsi berikut menggunakan definisi turunan.

Jawab:

Yang ini akan menjadi sedikit lebih berantakan sejauh aljabar berjalan. Namun, di luar itu akan bekerja dengan cara yang persis sama dengan contoh sebelumnya. Pertama, kita masukkan fungsi ke dalam definisi turunannya,yaitu

Perhatikan bahwa kami mengubah semua huruf dalam definisi agar sesuai dengan fungsi yang diberikan. Perhatikan juga bahwa kami menulis pecahan dengan cara yang jauh lebih kompak untuk membantu kami dengan pekerjaan itu.

Seperti masalah pertama, kita tidak bisa begitu saja mencolokkan $h=0$. Jadi, kita perlu sedikit menyederhanakan segalanya. Dalam hal ini kita perlu menggabungkan dua istilah dalam pembilang menjadi satu ekspresi rasional sebagai berikut.

Sebelum menyelesaikan ini mari kita perhatikan beberapa hal. Pertama, kami tidak melipatgandakan penyebutnya. Mengalikan penyebut akan terlalu mempersulit banyak hal, jadi mari kita tetap sederhana. Selanjutnya, seperti contoh pertama, setelah penyederhanaan kita hanya memiliki istilah dengan h di dalamnya yang tersisa di pembilang sehingga kita sekarang dapat membatalkan h out.

Jadi, setelah membatalkan h kita dapat mengevaluasi batas dan mendapatkan turunannya.

Sehingga turunan yang didapat adalah:

Contoh 3 Tentukan turunan dari fungsi berikut menggunakan definisi turunan.

Jawab:

Pertama-tama masukkan terlebih dahulu nilai fungsinya ke definisi turunan seperti yang telah kita lakukan dengan dua contoh sebelumnya.

Dalam masalah ini kita harus merasionalisasi pembilang. Anda ingat rasionalisasi pada bagian Aljabar bukan? Pada Aljabar Anda mungkin hanya merasionalisasi penyebut, tetapi Anda juga dapat merasionalisasi pembilang. Ingatlah bahwa dalam merasionalisasi pembilang (dalam hal ini) kita mengalikan pembilang dan penyebut dengan pembilang kecuali kita mengubah tanda antara dua istilah. Inilah pekerjaan rasionalisasi untuk masalah ini,

Sekali lagi, setelah penyederhanaan kita hanya memiliki h yang tersisa di pembilang. Jadi, batalkan h dan cari batasnya.

Jadi kita mendapatkan turunan yaitu,

Contoh 4 Tentukan nilai  $f^{\prime }\left(0\right)$ bagi $f\left(x\right)=\left|x\right|$.

Karena masalah ini meminta turunan pada titik tertentu, kami akan melanjutkan dan menggunakannya dalam pekerjaan kami. Itu akan membuat hidup kita lebih mudah dan itu selalu merupakan hal yang baik.

Jadi, colokkan ke definisi dan sederhanakan.

Kita harus melihat dua batas satu sisi dan mengingat bahwa